Διεγερμένο άτομο υδρογόνου
εκπέμπει κατά την αποδιέγερσή του φωτόνιο συγκεκριμένης συχνότητας, το οποίο,
όταν περνά μέσα από νερό με δείκτη διάθλασης n=3/1,6 για την παραπάνω
συχνότητα, έχει μήκος κύματος λν=1000nm.
α. Ποιο είναι το μήκος κύματος
λο του φωτονίου στο
κενό;
β. Πόση είναι η ενέργειά του Eφωτ μετρημένη σε eV;
γ. Από ποια στάθμη στη n=3 έγινε η αποδιέγερση, που έδωσε το
παραπάνω φωτόνιο;
δ. Πόσοι είναι οι δυνατοί
τρόποι αποδιέγερσης από την παραπάνω στάθμη και πόσα διαφορετικά φωτόνια
μπορούν να εκπεμφθούν σ’ αυτούς; Ποιο από αυτά τα φωτόνια έχει το μικρότερο μήκος
κύματος και πόσο είναι αυτό;
Δίνονται co=3×108m/s,
h=6,6×10-34J×s, E1=-13,6eV, 1eV=1,6×10-19J.
Απάντηση:
Τρίτη 29 Ιανουαρίου 2013
Σάββατο 26 Ιανουαρίου 2013
Χρονική καθυστέρηση μονοχρωματικής ακτίνας
Μονοχρωματική
ακτίνα διαπερνά κάθετα στρώμα γυαλιού πάχους d και στη συνέχεια βγαίνει στον αέρα (nαέρα=1), όπου διανύει επίσης διαδρομή d. Αν για να διανύσει τη διαδρομή d στο γυαλί χρειάζεται 50% περισσότερο
χρόνο απ’ ότι για να διανύσει την αντίστοιχη διαδρομή d στον αέρα, να υπολογίσετε:
α.
το δείκτη διάθλασης nγ του γυαλιού για την παραπάνω ακτίνα.
β.
το μήκος κύματός της λγ στο γυαλί, αν η συχνότητά της είναι f=5×1014Hz.
γ.
την απόσταση d,
αν ο ολικός χρόνος για την παραπάνω διαδρομή είναι 5ns.
δ.
σε πόσα μήκη κύματός της λγ αντιστοιχεί το πάχος d του γυαλιού.
Διαδοχικές διαθλάσεις ακτίνας
Μονοχρωματική
ακτίνα εκπέμπεται από πηγή και, αφού διανύσει στον αέρα (nαέρα=1) απόσταση d=107λο σε χρόνο to=10-8s, εισέρχεται σε νερό, όπου διανύει
επίσης απόσταση d=1,25×107λν,
και μετά σε γυαλί, όπου διανύει επίσης απόσταση d=1,5×107λγ.
Να βρείτε:
α.
τη συχνότητα f
της ακτίνας.
β.
τους δείκτες διάθλασης nν του νερού και nγ του γυαλιού για την παραπάνω ακτίνα.
γ. το χρόνο t,
που χρειάζεται για να διανύσει την παραπάνω συνολική διαδρομή.
δ. Πόση είναι η %
μεταβολή της ταχύτητας της ακτίνας κατά το πέρασμά της από το νερό στο γυαλί;
Παρασκευή 25 Ιανουαρίου 2013
ΕΟΚ και μέση διανυσματική ταχύτητα
Ο
Άρης ξεκίνησε το πρωί από το σπίτι του (έστω t=0) για να πάει με τα πόδια στη
δουλειά.
Περπάτησε
25s και έφτασε στο περίπτερο της πλατείας, που απέχει από το σπίτι
του 20m.
Εκεί
σταμάτησε για μισό λεπτό για να φάει τη σοκολάτα που αγόρασε και στη συνέχεια
προχώρησε για τη δουλειά του.
Μετά από 100s είχε απομακρυνθεί 80m
από το περίπτερο και
έφτασε στο μπακάλικο, όταν συνειδητοποίησε ότι ξέχασε το πορτοφόλι του εκεί που
έβγαλε να πληρώσει τη σοκολάτα.
Έτσι
ακαριαία γύρισε και μέσα σε 20s
έφτασε στο περίπτερο για
να το πάρει.
Α. Να διαβάσεις ξανά το παραπάνω
κείμενο και σημειώσεις στο σχήμα:
1. το διάνυσμα της ταχύτητας του Άρη
σε κάθε τμήμα της παραπάνω κίνησης.
2. τη θέση του περίπτερου και του μπακάλικου
με σημείο αναφοράς (θέση χ=0) το σπίτι του Άρη.
3. τις χρονικές στιγμές που ο Άρης:
έφτασε στο περίπτερο, ξεκίνησε από εκεί αφού έφαγε τη σοκολάτα, έφτασε στο
μπακάλικο και, τέλος, επέστρεψε στο περίπτερο να πάρει το πορτοφόλι.
Β.
Να υπολογίσεις την ταχύτητα του Άρη στην κίνηση:
1. από το σπίτι του μέχρι το
περίπτερο,
2. από το περίπτερο μέχρι το
μπακάλικο,
3. από το μπακάλικο μέχρι να
επιστρέψει στο περίπτερο, αν
θεωρήσουμε ότι αυτή είναι σταθερή σε κάθε τμήμα της κίνησης.
Γ.
Να υπολογίσεις τη μέση διανυσματική ταχύτητα του Άρη για την παραπάνω κίνηση.
Δ.
Να κάνεις τα διαγράμματα ταχύτητα-χρόνου και θέσης-χρόνου για την παραπάνω
κίνηση.
Πέμπτη 24 Ιανουαρίου 2013
Τρεις ασκήσεις στο Φως
Άσκηση 1η
Μονοχρωματική
ακτίνα έχει μήκος κύματος λγ=400nm, όταν διαδίδονται σε γυαλί με δείκτη διάθλασης nγ=1,5 για
την παραπάνω ακτίνα. Να βρείτε:
α.
αν η ακτίνα είναι ορατή.
β.
τη συχνότητά της f, αν σε t=5×10-14s διανύει διαδρομή ίση με 25 μήκη κύματος.
γ.
την ενέργεια Ε, που μεταφέρουν Ν=108 φωτόνιά της.
Δίνεται
h=6,63×10-34J×s.
Άσκηση 2η
Η
συχνότητα μονοχρωματικής ακτινοβολίας είναι f=6×1014Hz. Η ακτίνα περνά από τον αέρα (nαέρα=1) σε
διαφανές υλικό, οπότε το μήκος κύματός της μεταβάλλεται κατά το 1/5 της αρχικής του τιμής. Να υπολογίσετε:
α.
τα μήκη κύματός της λο και λ στο κενό και στο διαφανές υλικό.
β.
το δείκτη διάθλασης n του υλικού για τη συγκεκριμένη
ακτίνα.
γ.
την ταχύτητά της c στο διαφανές υλικό.
δ.
την ισχύ P φωτεινής πηγής, που εκπέμπει 1020
φωτόνια της παραπάνω ακτινοβολίας ανά δευτερόλεπτο.
Δίνονται co=3×108m/s,
h=20/3 ×10-34J×s.
Άσκηση 3η
Μονοχρωματική ακτινοβολία, που διαδίδεται στον αέρα (nαέρα=1), περνά διαδοχικά από γυαλί και νερό. Αν η ακτίνα έχει μήκος κύματος λν=600nm στο νερό και λγ=540nm στο γυαλί, να υπολογίσετε:
Μονοχρωματική ακτινοβολία, που διαδίδεται στον αέρα (nαέρα=1), περνά διαδοχικά από γυαλί και νερό. Αν η ακτίνα έχει μήκος κύματος λν=600nm στο νερό και λγ=540nm στο γυαλί, να υπολογίσετε:
α.
το λόγο των δεικτών διάθλασης του νερού και του γυαλιού για την παραπάνω
ακτίνα.
β.
το δείκτη διάθλασης nν του νερού, αν κατά την έξοδό της από το νερό στον
αέρα το μήκος κύματός της μεταβάλλεται κατά το 50% της αρχικής του τιμής.
γ.
το δείκτη διάθλασης nγ του γυαλιού και την ταχύτητα διάδοσής της cγ στο
γυαλί
δ.
το λόγο των διαδρομών, που διανύει σε χρόνο μιας περιόδου στο νερό και το γυαλί,
αντίστοιχα.
Δίνεται
co=3×108m/s.
Τετάρτη 23 Ιανουαρίου 2013
Ερωτήσεις για το τρέχον κύμα
Ερώτηση 1η
Σε ένα γραμμικό μέσο διαδίδεται προς τα δεξιά εγκάρσιο αρμονικό
κύμα, του οποίου το στιγμιότυπο σε κάποια χρονική στιγμή t1 φαίνεται στο σχήμα.
Ποια από τις παρακάτω προτάσεις
είναι σωστή;
α. Η απόσταση ΚΝ είναι ίση με
λ/2, όπου λ το μήκος κύματος του κύματος.
β. Εκείνη τη στιγμή το σημείο Λ
κινείται προς τη θέση ισορροπίας του.
γ. Τα σημεία Κ και Μ έχουν
διαφορά φάσης π/2.
δ. Τα σημεία Κ και Ν
ταλαντώνονται σε συμφωνία φάσης.
Ερώτηση 2η
Η εξίσωση ταλάντωσης ενός
μορίου Μ γραμμικού ελαστικού μέσου, στο οποίο διαδίδεται εγκάρσιο αρμονικό
κύμα, είναι yΜ=Aημ2π(t-2,25) στο S.I. Τη
χρονική στιγμή t=2s το
σημείο Μ βρίσκεται:
α. στη θέση ισορροπίας του.
β. στη θέση με απομάκρυνση y=-A.
Να επιλέξετε το σωστό και να
αιτιολογήσετε την επιλογή σας.
Ερώτηση 3η
Η εξίσωση αρμονικού κύματος
είναι y=Αημ2π(t -χ/λ) στο S.I. Ποιο από τα παρακάτω στιγμιότυπα αντιστοιχεί στη
χρονική στιγμή t=2,5s; Να αιτιολογήσετε την επιλογή σας.
Ερώτηση 4η
Σε ένα γραμμικό ελαστικό
μέσο διαδίδεται εγκάρσιο αρμονικό κύμα. Το στιγμιότυπο του κύματος τη στιγμή t1=2,5T φαίνεται
στο παρακάτω διάγραμμα.
Να χαρακτηρίσετε με «ΣΩΣΤΟ» ή
«ΛΑΘΟΣ» τις παρακάτω προτάσεις αιτιολογώντας την επιλογή σας.
α. Η αρχική φάση ταλάντωσης της
πηγής του κύματος, που βρίσκεται στη θέση χ=0, είναι φο,Ο=π rαd.
β. Το μήκος κύματος του κύματος
είναι λ=15cm.
γ. Τα σημεία Κ και Λ
ταλαντώνονται σε αντίθεση φάσης.
Τρίτη 22 Ιανουαρίου 2013
Ερωτήσεις για τα στάσιμα
Ερώτηση 1η
Σε μια χορδή δημιουργείται
στάσιμο κύμα. Στη θέση χ=0 υπάρχει μία κοιλία του στάσιμου. Τα σημεία της
χορδής, που ταλαντώνονται με πλάτος ίσο με το πλάτος των κυμάτων που συνέβαλαν
και έδωσαν το στάσιμο, βρίσκονται εκατέρωθεν των κοιλιών κατά:
α.
λ/4 β. λ/6 γ. λ/3 δ. λ/12
και των
δεσμών κατά:
α.
λ/4 β. λ/6 γ. λ/3 δ. λ/12
Ερώτηση
2η
Μία χορδή
έχει το ένα άκρο στερεωμένο και το άλλο άκρο ελεύθερο. Κατά μήκος της χορδής
δημιουργείται στάσιμο κύμα με κ κοιλίες. Στο ελεύθερο άκρο της χορδής
σχηματίζεται κοιλία.
Α… Το
μήκος L της χορδής είναι:
α. L=κλ/2
β. L=(2κ+1)λ/4
γ. L=(κ-1)λ/2 + λ/4
δ. L=κλ/2 + (2κ+1)λ/4
Β… Αν ο
αριθμός των δεσμών είναι μ, τότε ισχύει:
α. μ=κ β. μ=κ-1 γ. μ=κ+1 δ.
μ=2κ
Γ… Αν
τριπλασιάσουμε τη συχνότητα των κυμάτων που συμβάλλουν και δίνουν το στάσιμο
και στο ελεύθερο άκρο σχηματίζεται και πάλι κοιλία, τότε ο αριθμός των κοιλιών
που σχηματίζονται συνολικά τώρα στη χορδή θα είναι
α. κ΄=3κ-1 β. κ΄=3κ γ. κ΄=κ-3 δ. κ΄=κ/3
Ερώτηση
3η
Ένα
στάσιμο κύμα περιγράφεται από την εξίσωση
y=8συν(2πχ/λ)ημ2πt
(τα χ και y σε cm, το t σε s)
Κάποια
χρονική στιγμή t το
στιγμιότυπο του στασίμου φαίνεται στο παρακάτω διάγραμμα.
Να κατασκευάσετε το
στιγμιότυπο του στασίμου τη χρονική στιγμή t΄=t+1/3s.
Δευτέρα 21 Ιανουαρίου 2013
Τρέχον κύμα σε γραμμικό ελαστικό μέσο
Ένα
εγκάρσιο αρμονικό κύμα διαδίδεται κατά μήκος γραμμικού ελαστικού μέσου με
ταχύτητα u=100cm/s. Θεωρούμε ότι το μέσο ταυτίζεται με το άξονα χ’χ
και ότι το κύμα διαδίδεται κατά τη θετική φορά. Τη στιγμή t=0, το σημείο Ο, που βρίσκεται στη θέση χ=0, αρχίζει
να ταλαντώνεται με εξίσωση
y=2ημ10πt (το y σε cm, το t σε s).
Ένα
σημείο Μ του μέσου βρίσκεται στη θέση χΜ=80cm
από το Ο.
Α…
Να γράψετε την εξίσωση της απομάκρυνσης του Μ από τη θέση ισορροπίας του και να
υπολογίσετε την τιμή της τη στιγμή t1=35/40s.
Β…
Να κάνετε τη γραφική παράσταση της φάσης του σημείου Μ συναρτήσει του χρόνου.
Γ…
Να βρείτε ποια χρονική στιγμή t2 το σημείο Μ θα
βρίσκεται για πρώτη φορά στη θέση της μέγιστης θετικής απομάκρυνσής του.
Δ…
Να βρείτε για τη στιγμή t2 ποια σημεία του
μέσου που βρίσκονται στο θετικό ημιάξονα θα έχουν απομάκρυνση y=+1cm από τη θέση
ισορροπίας τους με θετική ταχύτητα.
Ε…
Να κάνετε το στιγμιότυπο του κύματος τη στιγμή t2 για τα σημεία
του θετικού ημιάξονα.
Κυριακή 20 Ιανουαρίου 2013
Χρώμα, μια ψευδαίσθηση του ματιού
Ποιο
αντικείμενο θα μπορούσε κάτω από προϋποθέσεις να γίνει αόρατο;
α.
Μπλε αντικείμενο σε λευκό φόντο που φωτίζεται
με λευκό φως και παρατηρείται μέσα από μπλε φίλτρο.
β.
Μπλε αντικείμενο σε κίτρινο φόντο που φωτίζεται με λευκό φως
και παρατηρείται μέσα από κόκκινο φίλτρο.
γ.
Πράσινο αντικείμενο σε κόκκινο φόντο που φωτίζεται με κόκκινο φως.
δ.
Λευκό αντικείμενο σε πορτοκαλί φόντο που φωτίζεται με πορτοκαλί φως.
Φαινόμενη ανύψωση σημείου
Ένα
γυάλινο διάφανο πλακίδιο με πάχος d και
μεγάλο μήκος βρίσκεται πάνω σε οριζόντιο τραπέζι. Ένας παρατηρητής παρατηρεί από
τον αέρα πάνω από το γυάλινο πρίσμα ένα κόκκινο σημείο Α βαμμένο πάνω στο
τραπέζι.
1. Αν η παρατήρηση γίνεται σχεδόν κατακόρυφα (από μικρή γωνία), να δείξετε ότι η
φαινόμενη ανύψωση του σημείου Α είναι h=(n–1)×d/n, όπου n o
δείκτης
διάθλασης του πλακιδίου για τη μονοχρωματική ακτίνα που αντιστοιχεί στο χρώμα
του σημείου Α.
2. Να δειχθεί
ότι, αν η γυάλινη πλάκα ανυψωθεί κατά h’ πάνω από το τραπέζι, τότε το σημείο Α θα φαίνεται και
πάλι ανυψωμένο κατά h, όπως και πριν.
Δίνεται ότι
για μικρή γωνία φ ισχύει: ημφ»εφφ.
Παρασκευή 18 Ιανουαρίου 2013
Εξαναγκασμένη ταλάντωση και ενέργειες
Στην
εξαναγκασμένη ταλάντωση ενός συστήματος ελατηρίου-μάζας η μέγιστη δυναμική
ενέργεια ταλάντωσης Umax= ½ mωο2A2 είναι ίση με την μέγιστη κινητική ενέργεια Kmax= ½ mωδ2Α2 μόνο
στην περίπτωση που η συχνότητα του διεγέρτη είναι ίση με την ιδιοσυχνότητα του
συστήματος. Πού οφείλεται αυτή η διαφορά;
Στην εξαναγκασμένη ταλάντωση ενός συστήματος ελατηρίου-μάζας ασκούνται οι δυνάμεις:
Στην εξαναγκασμένη ταλάντωση ενός συστήματος ελατηρίου-μάζας ασκούνται οι δυνάμεις:
η
ελαστική δύναμη -kx,
με k=mωο2, η δύναμη απόσβεσης
και η δύναμη από το διεγέρτη, τη συνισταμένη των οποίων ονομάζω έστω F’.
Έτσι από
το 2ο νόμο του Newton για την
κίνηση έχουμε
–kx + F’= mα και επειδή α=–ωδ2x
–kx + F’= – mωδ2x.
F’= -m(ωδ2-ω02)x
Τότε:
Αν ωδ>ωο τότε F’=–m(ωδ2–ωο2)×x,
οπότε:
όταν x>0
τότε F’<0 ενώ όταν x<0 τότε F’>0
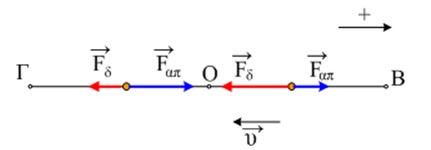
Έστω λοιπόν ότι το σώμα ξεκινά
από την ακραία θέση Β, στην οποία έχει μια ορισμένη τιμή δυναμικής ενέργειας Umax και
κινείται προς τα αριστερά. Στο σχήμα εμφανίζονται οι δυνάμεις που ασκούνται στο
σώμα.
Το έργο της συνισταμένης (των Fδ και
Fαπ) F’ είναι θετικό στην κίνηση προς τη Θ.Ι. Ο και
αρνητικό προς την ακραία θέση Γ, οπότε η μέγιστη κινητική ενέργεια θα είναι μεγαλύτερη
από τη μέγιστη δυναμική ενέργεια κατά το έργο τη F΄.
Δείτε όλη την απόδειξη από εδώ.
Μια συνθήκη για ολική ανάκλαση
Έστω
μονοχρωματική ακτίνα και τριγωνικό διάφανο πρίσμα, που παρουσιάζει δείκτη
διάθλασης n
και κρίσιμη γωνία ως
προς τον αέρα θκρ για την παραπάνω ακτίνα.
Η
ακτίνα προσπίπτει από τον αέρα υπό γωνία θ στην έδρα ΑΒ του πρίσματος, το
διαπερνά και είναι έτοιμη να εξέλθει από αυτό και πάλι στον αέρα από την έδρα
ΑΓ, όπως φαίνεται στο παραπάνω σχήμα.
Να
δείξετε ότι: αν η γωνία Α του πρίσματος είναι μεγαλύτερη από το διπλάσιο της
κρίσιμης γωνίας, η ακτίνα θα πάθει ολική ανάκλαση στην έδρα ΑΓ.
Δίνεται
nαερ=1.
Πέμπτη 17 Ιανουαρίου 2013
Συμβολή κυμάτων - Κροσσοί ενίσχυσης και απόσβεσης
Στα σημεία Π1 και Π2 της επιφάνειας ενός υγρού βρίσκονται δύο
σύγχρονες πηγές αρμονικών κυμάτων, που ταλαντώνονται με συχνότητα f και πλάτος A. Δύο σημεία Μ και Ν του ευθυγράμμου
τμήματος Π1Π2 έχουν αντίστοιχα αποστάσεις από τις δύο
πηγές που ικανοποιούν τις σχέσεις:
Μ:
(Π2Μ) – (Π1Μ)=3λ και
Ν:
(Π1Ν) – (Π2Ν)=3λ/2.
Να
επιλέξετε το σωστό σε κάθε περίπτωση και να αιτιολογήσετε την επιλογή σας:
Α…
Τα σημεία του τμήματος Π1Π2 που βρίσκονται μεταξύ των Μ
και Ν και ταλαντώνονται με μέγιστο πλάτος είναι:
α. 1 β.
2 γ. 3 δ. 4
Β…
Η απόσταση ΜΝ είναι ίση με:
α. 3λ/4 β. 5λ/4 γ.
7λ/4 δ. 9λ/4
Γ… Η
απομάκρυνση του Μ από τη θέση ισορροπίας του τη στιγμή που το μέσο Ο του ΠιΠ2
ξεκινά την ταλάντωσή του θα είναι:
α. +Α β. –Α γ.
0 δ. +Α/2
Θεωρούμε
ως στιγμή t=0
τη στιγμή που τα κύματα φτάνουν στο Ο.
Τετάρτη 16 Ιανουαρίου 2013
Εκτροπή ακτίνας από κυβικό πρίσμα
Μια
μονοχρωματική ακτίνα προσπίπτει στο κέντρο μιας έδρας κυβικού πρίσματος πλευράς d, υπό γωνία 45ο ως προς
το επίπεδο της έδρας, όπως φαίνεται στο σχήμα.
Να
δείξετε ότι η ακτίνα θα βγει από το πρίσμα από την απέναντι έδρα σε απόσταση από
την κορυφή Β ίση με
και
να υπολογίσετε κατά πόσο θα εκτραπεί από την αρχική της κατεύθυνση διάδοσης
μετά τη διέλευσή της από το πρίσμα.
Δίνονται
οι δείκτες διάθλασης του αέρα και του πρίσματος για την ακτίνα:
Τρίτη 15 Ιανουαρίου 2013
Σάββατο 12 Ιανουαρίου 2013
Διαγώνισμα στο Φως 2012
Θέμα 2ο
Β1) Στο παρακάτω σχήμα φαίνεται η τομή ενός τριγωνικού πρίσματος και μια μονοχρωματική ακτίνα που προσπίπτει στη μια έδρα του προερχόμενη από τον αέρα.
Β1) Στο παρακάτω σχήμα φαίνεται η τομή ενός τριγωνικού πρίσματος και μια μονοχρωματική ακτίνα που προσπίπτει στη μια έδρα του προερχόμενη από τον αέρα.
Να χαράξετε την πορεία της ακτίνας μέχρι την έξοδό της από το πρίσμα από
την έδρα ΑΓ.
Στο σχήμα να σημειώσετε τις γωνίες εκτροπής της ακτίνας κατά την είσοδο
και την έξοδό της από το πρίσμα, καθώς και τη συνολική γωνία εκτροπής.
Δείτε όλο το διαγώνισμα από εδώ.
Εγγραφή σε:
Αναρτήσεις (Atom)